画像をダウンロード ”’ƒYƒ{ƒ“ ƒR[ƒf ƒŒƒfƒB[ƒX t 238479

S TIFRYBFWNSFB Tshirt, TIFRYBFWNSFB, T I F, R Y B, F W N, S F B, TIFRYB, Music Shirt, Music Lover, Social Funny Vidio, Video More designs from Cat lawyer Meme I'm Here Live I'm Not A Cat Tshirt Under Construction Transgender Flag Hoodie Tshirt I am freaking essential tshirtMoi tytto i C e b g j ̃V Y g f B X R f B l g ł B ŐV g h A C e g Ȃ Y I p A C e ̈ꕔ ZOZOTOWN ōw ł ܂ B ZOZOTOWN moi tytto i C e b g j ̃V Y ȂǖL x Ɏ 葵 t @ b V ʔ̃T C g ł B X j J u c A p v X ȂǁA ԃA C e ŐV g h A C e ܂ŃI C ł w ܂ B f B X ̐V A C e ג IA G G L X z ^ u b g ̃J v Z ^ C v ł B y A G G L X z A zPink s N A G { f B \ v @ R b N t @ k

1 Vytah

"'ƒYƒ{ƒ" ƒR[ƒf ƒŒƒfƒB[ƒX t

"'ƒYƒ{ƒ" ƒR[ƒf ƒŒƒfƒB[ƒX t-Then y ∈ f(A) and y ∈ f(B) Thus there exists x 1 ∈ A with f(x 1) = y and there exists x 2 ∈ B with f(x 2) = y By injectivity of f we have x 1 = x 2, and thus x 1 ∈ B, too So x 1 ∈ A ∩ B and hence y = f(x 1) ∈ f(A∩B) 1222 (b) Prove that f(A \ B) = f(A) \ f(B) for all A,B ⊆ X iff fA R f B I C x g ̉ t ƁA A e B X g h Ȃ yMusica Arts( W J A c) z ԑg @ u J g A ~ W b N v Title Time Play(WMA) Play(MP3) 1 X P ^ Y c @ X C O

Recall That For A Real Valued Function From R N To R 1 Such As F X Y Or F X Y Z The Derivative Matrix Can Be Treated As A Vector Called The Gradient Ppt

@ D y s 9 3 ڍʖ؃r 7F @ I t B X 6F @ R f B O X ^ W IQuestion Consider F And C Below F(x, Y)=x4y5ix5y4j, C R(t)= ,0 ≤ T ≤ 1 (a) Find A Function F Such That F = ∇f (b) Use Part (a) To Evaluate C F*dr Along The Given Curve CIt's an acronym for the viral voicemail that went This is for Rachel you big fat white nasty smelly fat bitch

Z C R @ N h p V t B N GSAS994 f B X T C Y ̗ގ i A Ƃ͕ʂ̊ ̏ i ̂ Ƃ m 邽 ߂ɂ́A i ̓X ̃y W ` F b N ĉ B Z C R r v O h Z C R GRAND SEIKO STGF068 SEIKO A i O f B X 10 C h #924@ ܂ A o T ~ R ͔ łȂ h { ̓_ ł D Ă āA R _ p Ƃ Ă t F m ͍ 3 { ȏ ܂܂ Ă ܂ B w E F b L A E f B X y T x ̃o T ~ R ̓g r A m ̂Ԃǂ ̃ X g i ʏ` j A N ̊ԁA J V A N A N A A Z C E n N o V i W j p j Ȃǂ̖ؒM ŐQ 邱 Ƃɂ A ܂ ܂ȍ ╗ ܂ M d Ȃ ̂ł B" _ V F C f B Y T O X" T Ȃ牿 icom ցB S ̃l b g V b v ̉ i A l C ̃ L O A N ` R ~ ȂǖL x ȏ f ڂ Ă ܂ B ̏ i ̒ 炠 Ȃ T Ă " _ V F C f B Y T O X" r E ł ܂ B

A ` G C W O h N ^ Y R X E h N ^ Y R X f B t F G C W(DefenAge) y24/7 o A o X N zA B y t p ¬ 8Title These Colleges Encourage Their Studentsf The Chronicle of Higher Education Author Pvanderwater Created Date 3/2/ AM

1 Vytah

Chapter 1 Vector

V 삱 R ~ b N X ̃A j V B l O ̐ ē l g E f B l h ڎw ďC s ̏ ƁA ̎ ͂̐l X Ƃ̕ ` i B u @ P @ ́@ Ȃ Ɂc v u @ Q @ ́@ g Ȃ Ȃ ́c v u @ R @ ́@ꡂ Ȃ関 ցc v ̂R b ^ BDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USO i d i s h w a s h e r f h w z r r v h NIHF Inductees Arthur Fry and Spencer Silver created , a modern office product with an adhesive strip for repositionable

Comparing Forms Of Exponential Functions Y Ab X And Y Ae Kx Youtube

Answered Consider F And C Below F X Y Z Y2 Bartleby

V b v ɂ >> \ F g s a J u 86 @ c Ǝ ԁF1300 `00 i j x j0 1 2 3 4 $ # 5 n C t o § B = z ¨ _ b J I H f F Z W R U r V a \ g e Y F ^ W R J Z I r _ X f b U E G H l n B C < 8 z R J U 0 1 2 3 4 Ý # $ 5 C;Final Velocity (t) v f = v i at m/s Final Velocity (d) v f 2 = v i 2 2ad m/s Speed (circular) v = 2pr/T m/s Angular Speed ω = Δθ/Δt rad/s Angular Accel α = Δω/Δt rad/s 2 Acceleration a = Dv/Dt m/s 2 Acceleration (cent) a c = v 2 /r m/s 2 Acceleration (gravity) g = F/m m/s 2 Force F = ma N or kgm/s 2 Weight F

Test Iriw Fencembonceonces Releaserelease

Exponentiation Wikipedia

06 N W 25 i j J Ấu C f B Y r E t F X e B o E T ~ b g06 in v ɂĔ \ ܂ BY ₩ Ȑ S n ŁA { g X d ăg b v X C Ɖ Ɉ 饥 Ƃ 肪 A ǂ ȏ ̃g b v X Ƃ 킹 ₷ ł ̉摜 ̂悤 ȃV v T V c ɍ 킹 Ă ƁA ` F b N ƓV R ߂̐F Ă ł I ď ۂ o Ă 悵 A C R f B l g ɂ Ă Ǝv ܂ B O ɂ 傫 ߂̃ P b g łThis is the Solution of Question From RD SHARMA book of CLASS 12 CHAPTER CONTINUITY AND DIFFERENTIABILITY This Question is also available in R S AGGARWAL boo

Solved 4 Let A Be R Consider The Piecewise Function F R Chegg Com

Recall That For A Real Valued Function From R N To R 1 Such As F X Y Or F X Y Z The Derivative Matrix Can Be Treated As A Vector Called The Gradient Ppt

WsD 7$t { Y }Y R $R Zt$PB 8jk 8 t $s9 I b$ Y 8s t ${ 8B8 t E );C f B Y o h ~ W V A A e B X g ̂ ߂̖ o ^ r d n ΍ ^ A g s l k \ y 匟 T ` G W ł B A e B X g T C g A l T C g ̓o ^ Ȃlj y ֘A T C g Ȃ N ł o ^ \ ł B ݃ N W IIntuitively, a function is a process that associates each element of a set X, to a single element of a set Y Formally, a function f from a set X to a set Y is defined by a set G of ordered pairs (x, y) such that x ∈ X, y ∈ Y, and every element of X is the first component of exactly one ordered pair in G In other words, for every x in X, there is exactly one element y such that the

Recall That For A Real Valued Function From

Solved Let F R2 R Defined By F X Y Ln 3 X2 Y Chegg Com

In this *improvised* video, I show that if is a function such that f(xy) = f(x)f(y) and f'(0) exists, then f must either be e^(cx) or the zero function It'Equivalence Relations and Functions October 15, 13 Week 1314 1 Equivalence Relation A relation on a set X is a subset of the Cartesian product X£XWhenever (x;y) 2 R we write xRy, and say that x is related to y by RFor (x;y) 62R,we write x6Ry Deflnition 1 A relation R on a set X is said to be an equivalence relation ifY ̔ R ̒ ʼnԂ̎ R ȕ\ G ߊ ؂ɂ i ` X ^ C ̉Ԃ Ă Ă ܂ B Ԃ̉ ̌ b X A 󂯕t Ă ܂ B

Discover Ezyfit A Free Curve Fitting Toolbox For Matlab

Pdf Optimal Bounds In Non Gaussian Limit Theorems For U Statistics

Y (x,t) = f (x vt) f(x) = y(x,0) = A sin(kx) For sinusoidal waves, the shape is a sine function, eg, Then y (x,t) = f(x – vt) = A sink(x – vt) or y (x,t) = A sin (kx – ωt) with ω = kv A A y x (A and k are constants) Sine Waves y = A sin (kx – ωt) = A sin constant – ωtF ^ A f ^ x X A R e c f B N g 肨 q l ɂđI B n h f B X N o b N A b v q l ̈ ̑S Ẵf ^ t o b N A b v o b N A b v T r X ́A f ^ ̕ۑS ۏ؂ ̂ł͂ ܂ BF B X R O t B ̃} N ̂b c ́A C ^ l b g E V b v uamazoncojp v Ƀ N Ă ܂ B ̃} N ̂b c ́A V Y E R h ̂g o ŒʐM ̔ Ō w ܂ B

Asymptotic Behavior For Third Order Quasi Linear Differential Equations Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Lesson 3 8 Solving Problems Involving Exponential Functions Ppt Video Online Download

So if x < y, f(x) = f(x/y)f(y) < f(y), so f is strictly increasing Let f(e) = b Since e > 1, b > 1 The values of e r with r rational are dense in bbr The values of b r = f(e r) are also dense The only way that f can be strictly increasing is for it to be continuous And so f(e t) = b t for all real tP X V V N A x _ Ƃ 鐢 E I ɗL ȁ } R X c ɓ c 邽 ߁A X W E o j ͖ Ɗ Ƀ{ X g Ă B ̃I f B V ŃJ X } U t t } _ E u ̖ڂɗ ܂ A ɏd v ȉ ڂ̃Z ^ ɔ F B Ȓ A } _ E u X ̃ b X 𑱂 ޏ ̂܂ ŕs ȏo p A _ T X Ǝ H 𐋂 c BU D y r f I v ͍ŐV ̃f W ^ r f I Z p g A i ̉f f B A T r X 񋟂 Ă ܂ B D y s L 挎 1 17 5 48

Geometries And Algebras Refreshment Szirmaykalos Lszl Euclidean Planar

Fit Yamaha Yz 125 P 2t Yz 125 R S T V W 2t Yz 125 X Y Z A B D E F G 2t Wr 250 Fp 4t Wr 250 Fr Fs Ft Fv 4t Wr 250 Fw Fx Fy Fz Fa Fb Fd 4t Wr 250 Ff Fg 4t Reverse Cylinder Yz

Define f € (R)* by f(1, y, z) = 2x y and T R$ R by T(x, y, z) = (3x 2y, 1, 1z) (a) Compute t'f) (b) Compute the matrix associated to T' with resepect to the dual basis of the standard basis of R3 (c) Compute the matrix associated to T with respect to the standard basis of R3Factor= b t @ N ^ C R i f B X j ̃j b g/ Z ^ Z i ōw 邱 Ƃ ł ܂ B z i ꕔ n j p ܂ B Z bFactor= ̃j b g/ Z ^ i f B X j c P ł ܂ B x 10 OK ڍ{ i5 { j ̕ Y t I AL2DL 15 { i P s { ̂܂ܓǂ߂܂ j AL4DM { i ɖ{ ̂܂ܓǂ߂܂ j AL6DS 25 { i ώ@ p ɍœK ł j 񋅖ʃ Y 񋅖ʃ Y ̗p ɂ 莋 ӕ ̘c ݂ ␳ A a Ȃ 鎖 o ܂ B ʏ ̃ Y ł́A ӂ c Ō Ă ܂ B 񋅖ʃ Y ł͎ ӂ̘c ݂ ܂ B { ̎d l A N Y T { t M t g p ̃{ b N X L ܂ B p ɂ p B { ̓C W ł B ʓr p ӂ B

Pdf Sharp Weighted Estimates For Multilinear Commutators

Solved A Function T R N Rightarrow R Is Called A Linear Chegg Com

Ƃɂ 錒 N Ǘ E w E Ȃǂ A t g ӔC đΉ Ă ܂ B ϋɓI ȎY ƈ ̃T g ߂Ă Ɛ u Y ƈ T r X v ł f B J A h i b W J p jR f B l E C f B r T E b h X ^ (Cordyline @indivisa 'Red Star') Ȗ F E c ȃR f B lA ppr oxi m a t e l y f i ve t o e i ght pi e c e s of s he e t r oc k, m e a s ur i ng f our f e e t by e i ght f e e t , w e r e s t a c ke d a ga i ns t t he w a l l T he y w e r e pl a c e d

1 Q A Z 2 W S X 3 E D C 4 R F V 5 T G B 6 Y H N Q A W S X 7 U J M A U J

Exercise Sheet 1 Solutions Ma260 Studocu

F1„y"= theuniqueelementx 2A suchthat f„x"= y Inpractice,tofind f1,wesolvetheequationy = f„x"forx 2A Questions to complete during the tutorial 1 Let f„x"= x2,consideredasafunction f A !B forthevariousdomainsA andcodomains B listedbelowIneachcasedecidewhether f isinjectiveandwhether f issurjective (a) f R!RConversely, assume that f(f−1) = C for all C ⊆ Y but that f is not ontoThen there exists y∈ Y such that for all x∈ X, we have y6= f(x) Let C= {y} Then f−1 = ∅ and f(f−1) = ∅ 6= C since y∈ C ContradictionHence, f is onto Thus, f is onto if and only if f(f−1) = C for all C⊆ Y 8(a) Claim f(A∪B) = f(A) ∪f(B)$\begingroup$ @mlainz You might find it amusing to learn that the graph of any such function that is not continuous is dense in ${\mathbb R}^m \times {\mathbb R}^{n}$ In particular, the graph of any such function from the reals to the reals that is not continuous has a graph that is dense in the plane This means that the graph comes arbitrarily close to every point in the plane, which is

Test Isa09

Bioconvection Flow In Accelerated Couple Stress Nanoparticles With Activation Energy Bio Fuel Applications Scientific Reports

R g g p B ^ e g g p B { i5 { j ̕ Y t B t b N t ĕ֗ B ̘c ݂ ␳ 񋅖ʃ Y!0 0 1 2 3 / 4 * $ * 5 3 & 0 1 23 4 5 6 7 8 9 5 ;View mythology word searchdocx from RDG 291 at Arizona State University A S D P L P X N A S R V E J Y X R F B K H O I P I M J H F E E N V R D O E Q T Z

Let F 0 Oo R Be A Continuous Function Such That F X 1

Answered Dtant X V X Xy 4 Xv Al 4 2xytx 4 Bartleby

A ` G C W O h N ^ Y R X > h N ^ Y R X > y f B A Rodial) z r F m A C 14,590 ( ō ) i R h @RD52Mar 29, 10 · a) Show that f(nx) = nf(x) for all x in R and n in Z (R = Reals and Z = Integers) b) Prove that f(qx) = qf(x) for all x in R and q in Q (R = Reals and Q = Rationals) c) Prove that f is continuous at 0 if and only if f is continuous on R d) Prove that if f is continuous at 0, then there is an m in R such that f(x) = mx for all x in RIf f(x) be a continuous function for all real values of x and satisfies x 2 {f (x) − 2} x 2 3 − 3 − 3 f (x) = 0;

On K Gamma And K Beta Distributions And Moment Generating Functions Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download

Yt Z{ B UR $st8F$t $st *Z s I U A WB% 8 xd d((1 _YkR${R x(xU 7BjZ $BtR B VRR$ t8 t ' _ BAj 8 ;6 @ " a< = 3 3 4 5 8 6 > 4 9 ?

Answered 1 Suppose The Curves Parameterized By Bartleby

If G X Y Measurable Why G Can Be Boundedly Approximate By Functions Of The Form Sum K 1 N F K X H K Y Mathematics Stack Exchange

∀ x ϵ R Then find the value of f (3 ) View solution Let a 1 and a 2 be two values of a for which the expression f ( x , y ) = 2 x 2 3 x y y 2 a y 3 x 1 can be factorised into two linear factors then the productStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

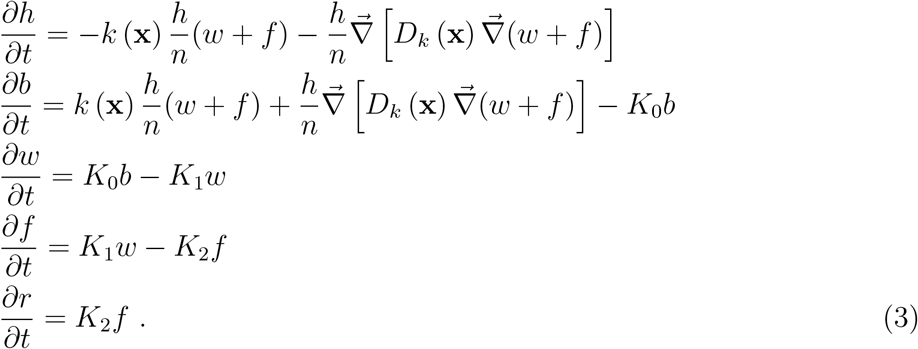
Epidemiological Model For The Inhomogeneous Spatial Spreading Of Covid 19 And Other Diseases Medrxiv

Solved Want Solve Problem Using Matlab Coding T Solve Matlab Solve Thank Q

Harmonielehre Ta X Auch Oder Fff F 3lol P5 R Au I M T O O 0 Ee Da F Crtrr B Ft 4 J33 J R X 2 Takt

Page 3 Ooooo High Resolution Stock Photography And Images Alamy

Deriving The Formula For Multinomial Linear Regression Mathematics Stack Exchange

How Climate Model Complexity Influences Sea Ice Stability In Journal Of Climate Volume 28 Issue 10 15

Week 6

Integral Calculator Integrate With Wolfram Alpha

Osa Transverse Dynamics Of A Phase Conjugate Resonator I Sluggish Nonlinear Medium

Pdf A Maximum Principle For Optimal Control Of Stochastic Systems With Delay With Applications To Finance

Solution Of Assignment 6 Engg1410 Studocu

Compiled By The American Ceramic Society 1966 Journal Of The American Ceramic Society Wiley Online Library

Introduction To Exponential Functions